WR Home      Topic Home	Chapter:  1  2
<Previous	Next>

---

Chapter 02

Basics of Animation and Forward Kinematics

Page 10

Forward Kinematics


Generally the FK problems are considered easier than the IK problems.

Developing software to control a robotic arm, needs the understanding of both.
Practically IK is required when moving the robot from one point to another, sometimes FK is used to verify the IK calculations.
Just like if 20 x 3 = 60 than it can be verified by 60 / 3 = 20

Students of Computer Science who have studied the transformations in Computer Graphics have already studied Forward Kinematics.
In order to understand the concept, let's start with a simple example.
Let us consider that there is a Point (x,y)

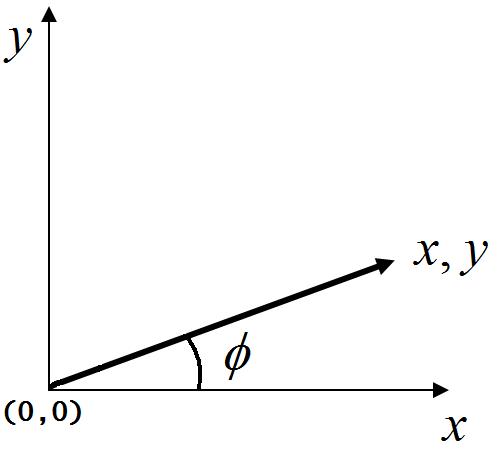
The Point(x,y) is making an angle φ with the x-axis
Suppose, the point is rotated θ degree, counter-clockwise, then what will be the new co-ordinates?
The point is at a distance r from the origin.

Then,
       x = r.cosφ
       y = r.sinφ

Because:

Now, If the point is rotated θ degrees counter-clockwise then,
let the new point will be (x', y')


and

       x' = r.cos( φ + θ )
       y' = r.sin( φ + θ )
Let r=1, unit distance from origin
then
       x' =  cos( φ + θ )
       y' =  sin( φ + θ )

       x' = cos( φ + θ ) = cosφ.cosθ - sinφ.sinθ = x.cosθ - y.sinθ
       y' = sin( φ + θ ) = cosφ.sinθ + sinφ.cosθ = x.sinθ + y.cosθ

Finally:
       x' = x.cosθ - y.sinθ
       y' = x.sinθ + y.cosθ

The above equations are very important, the gives the co-ordinates of the new point (x', y') if the point(x,y) is rotated θ degree counter-clockwise with respect to origin.

It is obvious that, if you need to rotate in clockwise direction then use (-θ) instead of (θ)


Now a simple excersise:
Question: If the Point(9,3) is rotated 23° counter-clockwise w.r.t. origin then what co-cordinate it will reach?

---

WR Home      Topic Home	Chapter:  1  2
<Previous	Next>