WR Home      Topic Home	Chapter:  1  2
<Previous	Next>

---

Chapter 02

Basics of Animation and Forward Kinematics

Page 11

Forward Kinematics: Rotation about an arbitrary point

The previous equations:
       x' = x.cosθ – y.sinθ
       y' = x.sinθ + y.cosθ
Can be written in matrix form as:

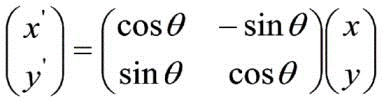
Which is one and the same thing, as shown in the following example:



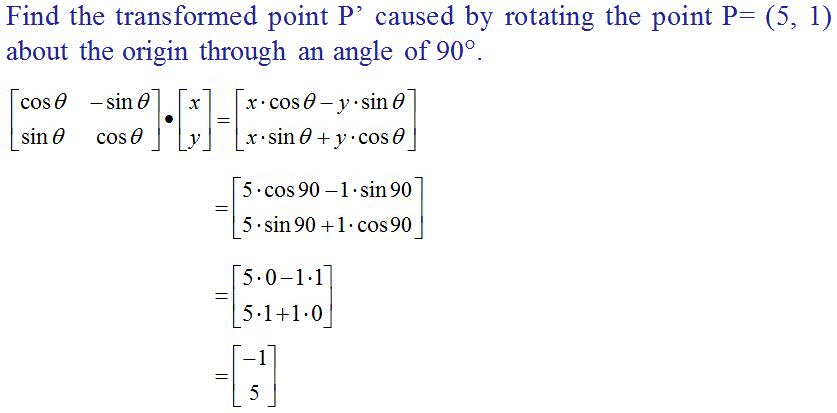
The matrix can also be written as (Homogeneous Coordinates):




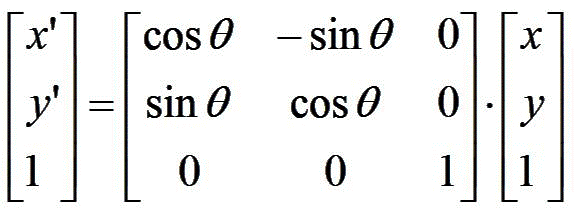
Previously the rotation was done w.r.t origin. Now if the Point(x,y) is to be rotated w.r.t a Point(xc, yc) then what could be done?
Where xc stands for x_center and yc stands for y_center

One easy way of achieving it is "shifting of origin"

1. Shift the point (xc, yc) to the origin
2. Rotate θ degree along the origin
3. Shift the result back to (xc, yc) from the origin

The equation shown below, combines the three steps:

Modified_Vector = Translate Rotate TrabslateBack Old_Vector



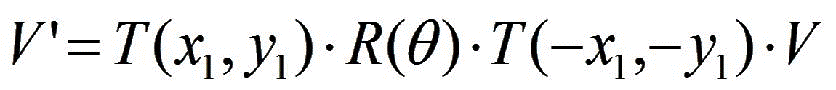
Or, in matrix form as:



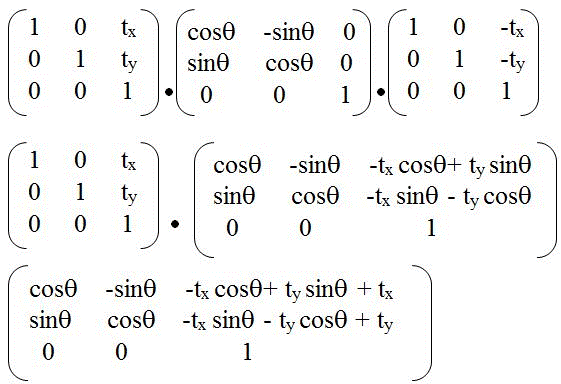
The following example helps in understanding the concept:



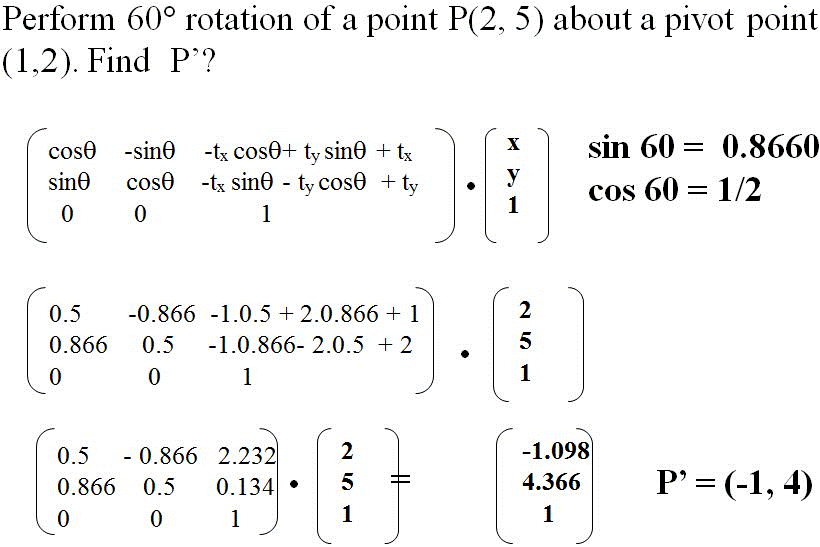
The Translate Rotate TrabslateBack matrices can be solved to form the following equation pair:



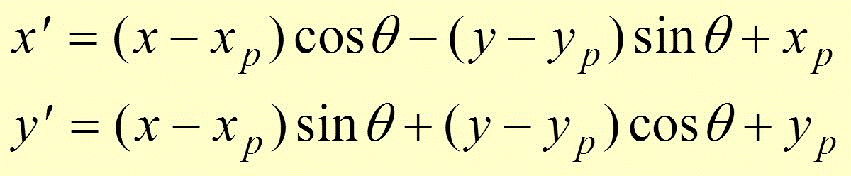
(xc, yc) is the center point or the pivot point, hence it is sometimes written as (xp, yp) as well.

Now, can you write a MATLAB® program to rotate a Point(x, y) w.r.t. another Point(xc, yc) to angle θ degree in a given direction.

Question: If the Point(9,3) is rotated 23° counter-clockwise w.r.t Point(2,6) then what co-cordinate it will reach?
HINT: Use the above equation pair.

x' = ( x - xc )cosθ - (y-yc)sinθ + xc
y' = ( x - xc )sinθ + (y-yc)cosθ + yc

x' = ( 9 - 2 )cos(23) - (3 - 6)sin(23) + 2
y' = ( 9 - 2 )sin(23) + (3 - 6)cos(23) + 6

Solving the above will give numeric value for the new point (x', y')
If the point was to be rotated clockwise instead, then simply replace (23) with (-23)

---

WR Home      Topic Home	Chapter:  1  2
<Previous	Next>