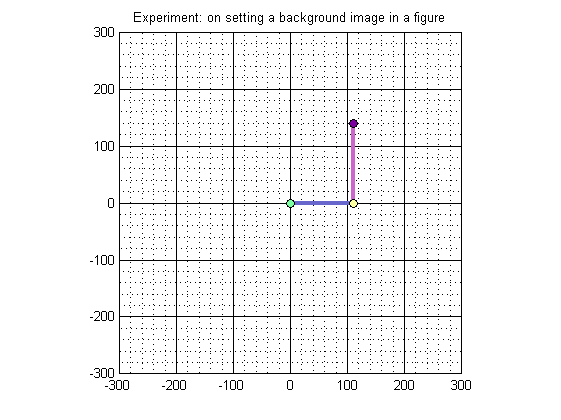
close all; clear; clc; global debugLevel_01; global L1; global L2; global SUM_L1_L2; debugLevel_01 = 1; L1 = 110.0; % Link_1 Length in mm L2 = 140.0; % Link_2 Length in mm SUM_L1_L2 = L1 + L2; initalizeArmCoordinates; printArmCoordinates; hf = figure('color','white'); % maximize(hf); axis equal maximum_x_limit = ceil(SUM_L1_L2/100)*100; maximum_y_limit = ceil(SUM_L1_L2/100)*100; minimum_x_limit = - ceil(SUM_L1_L2/100)*100; minimum_y_limit = - ceil(SUM_L1_L2/100)*100; % % % % Experiment: 1 % % % % Run the code. Let all Experiment(s) be commented % % % % Observe that Y increses 'Upwards', just like in Cartesian Co-ordinate % % % % System. % % % % Experiment: 2 % % % % To display the background image, read the images and show it % % % % U N C O M M E N T : % bk_image = imread('background_c.bmp'); % Read the image in an array % image(bk_image); % display it on the screen % % % % % % % % NOTES on Experiment: 2 % % % % PROBLEM 1: As soon as a background image is diaplayed, Y increase 'Downwards' % % % % unlike the Cartesian Co-ordinate System. This is because, in an image % % % % (or in computer graphics)Y-axis % % % % increases downwards! Also note that the robot arm looks reversed % % % % PROBLEM 2: Only a portion of image is displayed due to the axis % % % % limits set previously. % % % % Experiment: 3 % % % % Comment previous Experiment and uncomment this Experiment % % % % Problem 2 is solved here: use imagesc instead of image % bk_image = imread('background_c.bmp'); % imagesc(minimum_x_limit, minimum_y_limit, bk_image); % % % % % The above can can also be written as: % % % % % imagesc([minimum_x_limit, maximum_x_limit], [minimum_y_limit, maximum_y_limit], bk_image); % % % % Experiment: 4 % % % % Comment previous Experiment and uncomment this Experiment % % % % Problem 1 is solved here: Change y-axis direction to normal % bk_image = imread('background_c.bmp'); % imagesc([minimum_x_limit, maximum_x_limit], [minimum_y_limit, maximum_y_limit], bk_image); % set(gca,'ydir','normal'); % set the y-axis back to normal. % % % % PROBLEM 3: But the above solution introduces a new problem! % % % % The image gets inverted (and Robot arm gets normal) % % % % % % % % SOLUTION HINT: After all the image is stored in an array named % % % % 'bk_image' so why not 'flip' this array upside-down % % % % By using the functions like: % % % % fliplr, flipud, permute, rot90 and flipdim % % % % Experiment: 5 % % % % Comment previous Experiment and uncomment this Experiment % % % % Problem 3 is solved here: By using flipdim(I,1) % bk_image = imread('background_c.bmp'); % bk_image = flipdim(bk_image,1); % imagesc([minimum_x_limit, maximum_x_limit], [minimum_y_limit, maximum_y_limit], bk_image); % set(gca,'ydir','normal'); % set the y-axis back to normal. xlim([minimum_x_limit maximum_x_limit]); % Set X-axis range ylim([minimum_y_limit maximum_y_limit]); % Set Y-axis range % set(gca,'XTick',minimum_x_limit : 20 : maximum_x_limit); % set(gca,'YTick',minimum_y_limit : 20 : maximum_y_limit); grid on set(gca, 'GridLineStyle', '-'); grid(gca,'minor') set(gca,'XGrid','on','YGrid','on'); title('Experiment: on setting a background image in a figure'); % text(minimum_x_limit,minimum_y_limit,'string') hold on % causes subsequent plotting commands to add to what's already in the figure, instead of replacing it. % Draw the Robotic-Arm plot(lx(1:2), ly(1:2), 'color', [.4 .4 .8],'LineWidth',3); plot(lx(2:3), ly(2:3), 'color', [.8 .4 .8],'LineWidth',3); plot(lx(1),ly(1),'--mo', 'MarkerEdgeColor','k', 'MarkerFaceColor',[.49 1 .63], 'MarkerSize',6); plot(lx(2),ly(2),'--mo', 'MarkerEdgeColor','k', 'MarkerFaceColor',[.99 1 .63], 'MarkerSize',6); plot(lx(3),ly(3),'--mo', 'MarkerEdgeColor','k', 'MarkerFaceColor',[.49 0 .63], 'MarkerSize',6); saveas(gcf,'output.jpg')
lx[1] = 0.00 lx[2] = 110.00 lx[3] = 110.00 ly[1] = 0.00 ly[2] = 0.00 ly[3] = 140.00